3  Análisis de datos de contaminación del aire en la ciudad de Madrid

La aplicación de una metodología es fundamental en ciencia de datos, por ello, a continuación, se realiza un análisis estadístico de datos aplicando las seis fases de la metodología CRISP-DM.

Objetivo

• Analizar un caso de uso real en ciencia de datos con R utilizando la metodología CRISP-DM.

3.1 Entendimiento del negocio

Fase I: Comprensión de los problemas y desafíos asociados con la contaminación del aire

• Identificar las fuentes de contaminantes, evaluar los impactos en la salud humana y el medio ambiente y la formular políticas y regulaciones. Definición de los objetivos y requisitos:
• Establecer los objetivos específicos del análisis desde la perspectiva de valor añadido para la empresa o entidad pública: predecir los niveles de contaminación, identificar áreas de alto riesgo o evaluar la efectividad de medidas de control existentes.
• Determinar los requisitos de datos, como la disponibilidad de datos espaciales de calidad, datos meteorológicos y datos demográficos.

Se comienza formulando las preguntas de investigación que se consideran clave en el análisis. Por ejemplo:

• ¿Cuáles son las áreas con mayor nivel de contaminación del aire?
• ¿Qué factores contribuyen a la contaminación del aire en estas áreas?
• ¿Cómo ha evolucionado la contaminación del aire en estas áreas a lo largo del tiempo?

Una vez identificadas las preguntas clave, se definen los objetivos del análisis. Por ejemplo, en este caso, el objetivo principal es proporcionar mapas de predicción de calidad del aire para todo el municipio de Madrid.

Es importante tener en cuenta que los objetivos deben ser específicos, medibles y realistas. También deben estar alineados con los objetivos empresariales o públicos para proporcionar valor añadido.

3.2 Comprensión de los datos

Fase II: entendimimiento de los datos de calidad del aire

• Exploración de los datos:
  • Analizar la estructura de los datos, como las variables disponibles y sus tipos.
  • Realizar resúmenes estadísticos y análisis exploratorios, como la identificación de valores atípicos y la distribución de los datos.
• Visualización de los datos temporales:
  • Crear gráficos y mapas para visualizar la evolución temporal de la contaminación del aire.
  • Utilizar técnicas de visualización interactiva, como la creación de gráficos interactivos.
• Evaluación de la calidad de los datos:
  • Evaluar la calidad de los datos, la consistencia y la completitud.
  • Tratar los valores faltantes y los valores atípicos de manera apropiada.

Librerías y funciones en R

El paquete integrado de tidyverse es un buen aliado en esta tarea, ya que recoge las librerías para lectura, transformación y representación de los datos. Las librerías a tener en cuenta son:

• Lectura: reader.
• Manejo de datos: dplyr.
• Datos temporales: lubridate.
• Visualización: ggplot2, leaflet.

3.2.1 Obtención de los datos

El primer paso siempre es la obtención y carga de los datos. Los datos de la calidad de la ciudad de Madrid se encuentran disponibles en la página datos abiertos. Aquí, se seleccionan aquellos que tienen frecuencia diaria (disponibles aquí). Para obtener los datos de forma automatizada se utiliza la API proporcionada por la web de datos abiertos. Como base de obtención de los enlaces de descarga, se copia el enlace de la descarga en DECAT https://datos.madrid.es/egob/catalogo/201410-0-calidad-aire-diario.dcat. La definición y la estructura de los datos se encuentra en Intérprete de ficheros de calidad del aire.

library(tidyverse)
library(xml2)
library(vroom)

# Se guarda la URL RDF de DECAT de los datos
url <- "https://datos.madrid.es/egob/catalogo/201410-0-calidad-aire-diario.dcat"

# Se carga la página
page <- url %>%
  read_xml() %>%
  as_list()

# Se convierte en una lista e inspecciona para identificar la localización de los datos
location <- page[["RDF"]][["Catalog"]][["dataset"]][["Dataset"]]
location <- location[names(location) == "distribution"]


# Tras identificar se genera un tibble con el año como identificación y el link a los datos
links <-
  tibble(
    year = sapply(X = location, function(x) unname(unlist(
      x[["Distribution"]][["title"]][1]))),
    link = sapply(X = location, function(x) unname(unlist(
      x[["Distribution"]][["accessURL"]][1])))
  )

# Seleccionar el formato csv
links <- links %>% filter(str_detect(link, pattern = ".csv"))

# Añadir el nombre de fichero a descargar
links <- links %>% 
  mutate(file_name = paste0("datos_aire_madrid_", year, ".csv"))

# Descarga de los ficheros csv desde 2013
years <- links %>% filter(year >= "2013") %>% .$year

lapply(years, function(x) {
  file_x <- links %>%
    filter(year == x & str_detect(link, ".csv"))
  
  if (x == max(years)) {
    download.file(url = file_x$link,
                  destfile = paste0("data/",
                                    file_x$file_name))
  }
  
  if (!file.exists(paste0("data/", file_x$file_name))) {
    download.file(url = file_x$link,
                  destfile = paste0("data/",
                                    file_x$file_name))
  }
})

# Lectura de los ficheros
data <- vroom(paste0("data/", links %>% filter(year %in% years) %>% .$file_name))

# Conversión de viariables a numéricas
cols_to_numeric <-
  c(
    "PROVINCIA",
    "MUNICIPIO",
    "ESTACION",
    "MAGNITUD",
    "PUNTO_MUESTREO",
    "ANO",
    "MES",
    str_subset(names(data), pattern = '^D')
  )
data <- data %>%
  mutate(across(all_of(cols_to_numeric), as.numeric))

# Guardar datos brutos
write_rds(data, "data/data_raw.RDS")

# Transformar de datos transversales a longitudinales
air_mad <- data %>%
  gather(v, valor, D01:V31) %>%
  mutate(DIA = str_sub(v, 2, 3),
         v = str_sub(v, 1, 1))

air_mad <- air_mad %>%
  mutate(id = ESTACION,
         fecha = as.Date(paste(ANO, MES, DIA, sep = "-"))) %>%
  select(id, MAGNITUD, fecha, v, valor)

air_mad <- air_mad %>%
  unique() %>%
  pivot_wider(names_from = v, values_from = valor)
air_mad <- air_mad %>%
  mutate(valor = as.numeric(D)) %>%
  select(-D)

# Añadir información de diccionarios
station_names <- read_csv("dictionaries/station_names.csv")
magnitudes_names <- read_csv("dictionaries/magnitudes_names.csv")

air_mad <- left_join(air_mad, station_names, by = "id")
air_mad <- left_join(air_mad, magnitudes_names, by = "MAGNITUD")
air_mad <- air_mad %>% select(-MAGNITUD)

# Guardar los datos
write_rds(air_mad, "data/air_mad.RDS")

Se procede a la lectura de los datos obtenidos y procesados que se han guardado en el objeto air_mad.RDS. Posteriormente se consulta la clase del objeto.

library(tidyverse)
air_mad <- readr::read_rds("data/air_mad.RDS")
class(air_mad)

[1] "tbl_df"     "tbl"        "data.frame"

De acuerdo con la salida, se trata de un objeto de clase tibble, que forma parte del universo tidyverse. A continuación, se explora el conjunto de datos.

head(air_mad)

# A tibble: 6 × 12
     id fecha      V     valor id_name      longitud latitud zona  tipo  nom_mag
  <dbl> <date>     <chr> <dbl> <chr>           <dbl>   <dbl> <chr> <chr> <chr>  
1     4 2023-01-01 V       1   Plaza de Es…    -3.71    40.4 Inte… tráf… Dióxid…
2     4 2023-02-01 V       3   Plaza de Es…    -3.71    40.4 Inte… tráf… Dióxid…
3     4 2023-03-01 V       3   Plaza de Es…    -3.71    40.4 Inte… tráf… Dióxid…
4     4 2023-04-01 V       1   Plaza de Es…    -3.71    40.4 Inte… tráf… Dióxid…
5     4 2023-05-01 V       1   Plaza de Es…    -3.71    40.4 Inte… tráf… Dióxid…
6     4 2023-01-01 V       0.4 Plaza de Es…    -3.71    40.4 Inte… tráf… Monóxi…
# ℹ 2 more variables: nom_abv <chr>, ud_med <chr>

dim(air_mad)

[1] 559009     12

summary(air_mad)

       id            fecha                 V                 valor         
 Min.   : 4.00   Min.   :2013-01-01   Length:559009      Min.   :   -2.00  
 1st Qu.:18.00   1st Qu.:2015-07-16   Class :character   1st Qu.:    2.00  
 Median :38.00   Median :2018-01-26   Mode  :character   Median :   13.00  
 Mean   :34.95   Mean   :2018-02-03                      Mean   :   26.19  
 3rd Qu.:54.00   3rd Qu.:2020-08-02                      3rd Qu.:   36.00  
 Max.   :60.00   Max.   :2023-05-31                      Max.   :97396.00  
                 NA's   :157                                               
   id_name             longitud         latitud          zona          
 Length:559009      Min.   :-3.775   Min.   :40.35   Length:559009     
 Class :character   1st Qu.:-3.713   1st Qu.:40.41   Class :character  
 Mode  :character   Median :-3.689   Median :40.42   Mode  :character  
                    Mean   :-3.683   Mean   :40.43                     
                    3rd Qu.:-3.652   3rd Qu.:40.46                     
                    Max.   :-3.580   Max.   :40.52                     
                                                                       
     tipo             nom_mag            nom_abv             ud_med         
 Length:559009      Length:559009      Length:559009      Length:559009     
 Class :character   Class :character   Class :character   Class :character  
 Mode  :character   Mode  :character   Mode  :character   Mode  :character  
                                                                            
                                                                            
                                                                            
                                                                            

str(air_mad)

tibble [559,009 × 12] (S3: tbl_df/tbl/data.frame)
 $ id      : num [1:559009] 4 4 4 4 4 4 4 4 4 4 ...
 $ fecha   : Date[1:559009], format: "2023-01-01" "2023-02-01" ...
 $ V       : chr [1:559009] "V" "V" "V" "V" ...
 $ valor   : num [1:559009] 1 3 3 1 1 0.4 0.5 0.4 0.3 0.1 ...
 $ id_name : chr [1:559009] "Plaza de España" "Plaza de España" "Plaza de España" "Plaza de España" ...
 $ longitud: num [1:559009] -3.71 -3.71 -3.71 -3.71 -3.71 ...
 $ latitud : num [1:559009] 40.4 40.4 40.4 40.4 40.4 ...
 $ zona    : chr [1:559009] "Interior M30" "Interior M30" "Interior M30" "Interior M30" ...
 $ tipo    : chr [1:559009] "tráfico" "tráfico" "tráfico" "tráfico" ...
 $ nom_mag : chr [1:559009] "Dióxido de Azufre" "Dióxido de Azufre" "Dióxido de Azufre" "Dióxido de Azufre" ...
 $ nom_abv : chr [1:559009] "SO2" "SO2" "SO2" "SO2" ...
 $ ud_med  : chr [1:559009] "µg/m3" "µg/m3" "µg/m3" "µg/m3" ...

Warning

Existen paquetes como DataExplorer y dlookr que generan informes automáticos con los principales descriptivos.

¿Cómo han evolucionado la concentración de contaminantes del aire en la ciudad de Madrid en el periodo considerado? Realizar un primer gráfico de lineas para responder a esta pregunta sería muy esclarecedor.

library(lubridate)
air_mad %>%
  filter(V == "V") %>% 
  group_by(semana = floor_date(fecha, unit = "week"), nom_mag) %>%
  summarise(media_estaciones = mean(valor, na.rm = TRUE)) %>%
  ggplot(aes(x = semana, y = media_estaciones)) +
  geom_line(aes(color = nom_mag)) +
  geom_smooth(size = 0.5, color = "red") +
  labs(
    x = NULL, y = "(µg/m3)", title = "Evolución de contaminantes en Madrid",
    subtitle = "Concentración media semanal en las estaciones de medición",
    caption = "Fuente: Portal de datos abiertos del Ayuntamiento de Madrid"
  ) +
  theme_minimal() +
  theme(legend.position = "none") +
  facet_wrap(~nom_mag, scales = "free_y", ncol = 2)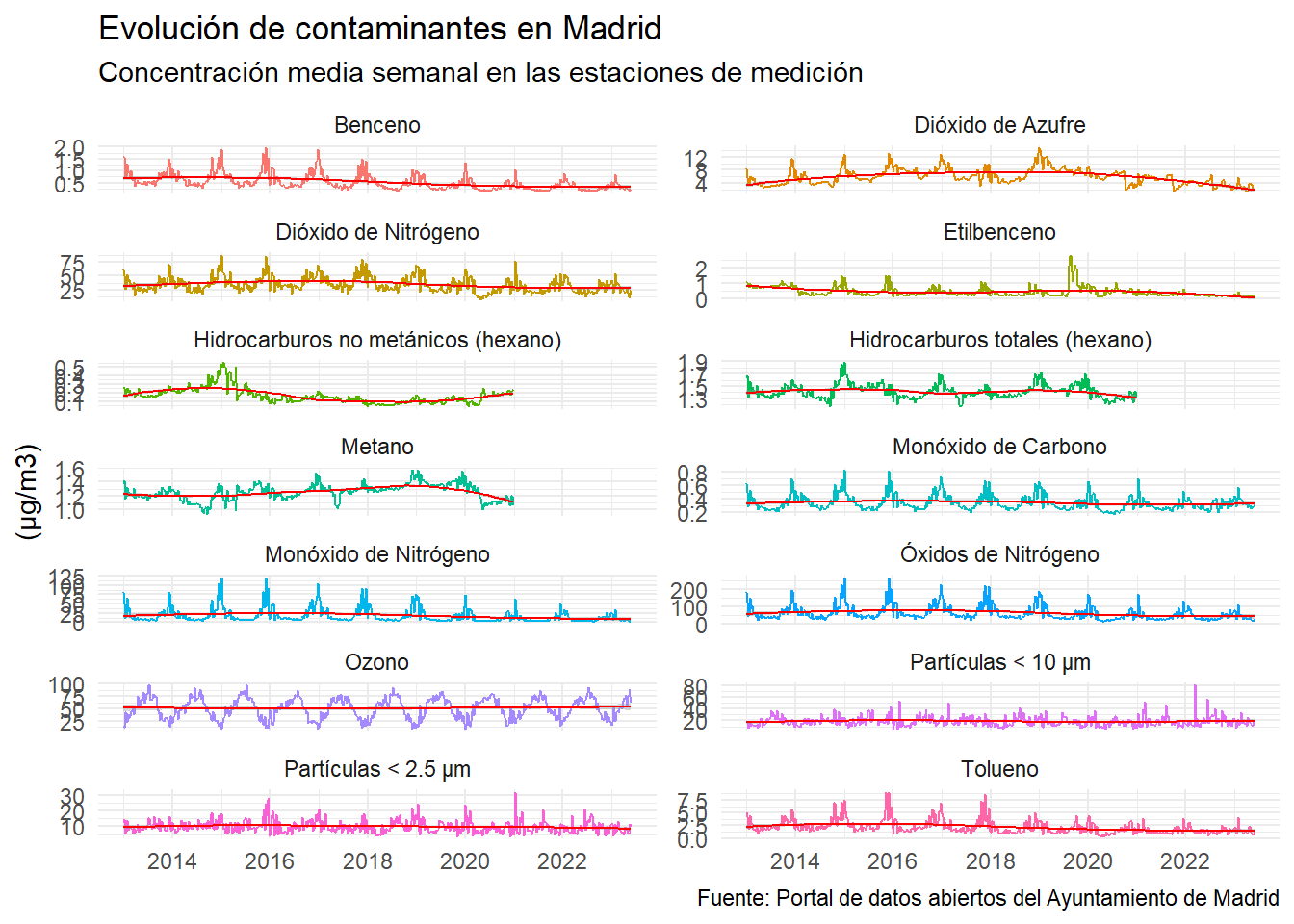

Figura 3.1: Evolución de contaminantes en Madrid (2013-2023)

Las emisiones de la mayoría de los contaminantes del aire han disminuido significativamente en las últimas décadas (véase Figure 3.1), sin embargo, sus concentraciones todavía superan los límites legales en la mayoría de los países, lo que indica que el control de la contaminación del aire sigue siendo un desafío para las sociedades modernas. Este análisis se centra en el dióxido de nitrógeno (NO2) por sus implicaciones directas en la ciudad de Madrid, además de por las siguientes razones de peso:

1. Impacto en la salud humana: el dióxido de nitrógeno son un contaminante del aire asociado a diversos problemas de salud, especialmente afecciones respiratorias. La exposición prolongada al NO2 puede causar irritación en las vías respiratorias, exacerbación de enfermedades pulmonares como el asma y aumentar el riesgo de infecciones respiratorias.

2. Fuente de emisión: el tráfico rodado es una de las principales fuentes de emisión de dióxido de nitrógeno en áreas urbanas. En ciudades con altos volúmenes de tráfico, como Madrid, se produce una considerable liberación de NO2 debido a la combustión de combustibles fósiles en los vehículos.

3. Regulaciones y límites: el dióxido de nitrógeno está sujeto a regulaciones y límites establecidos tanto a nivel nacional como internacional. Estos límites buscan controlar y reducir la concentración de NO2 en el aire para proteger la salud de la población y mejorar la calidad del aire en general.

4. Disponibilidad de datos: existen sistemas de monitoreo de calidad del aire que recopilan datos precisos sobre la concentración de dióxido de nitrógeno en tiempo real. En el caso de Madrid, el Ayuntamiento dispone de datos abiertos proporcionados por su red de estaciones de monitoreo, lo que facilita el análisis y seguimiento de los niveles de NO2 en la ciudad.

Teniendo en cuenta estas razones, el análisis de datos de contaminación se centrará en el dióxido de nitrógeno (NO2) para obtener información relevante sobre su impacto en la salud pública y evaluar el cumplimiento de los límites establecidos para este contaminante en la ciudad de Madrid (y concretamente, en la zonas de calidad del aire definidas por el ayuntamiento).

plot_air_mad <- air_mad %>%
  filter(V == "V" & nom_abv == "NO2" & fecha >= "2018-01-01") %>% 
  group_by(fecha, nom_mag, zona) %>%
  summarise(media_estaciones = mean(valor, na.rm = TRUE)) %>%
  ggplot(aes(x = fecha, y = media_estaciones)) +
  geom_line(aes(color = zona)) +
  geom_smooth(size = 0.5, color = "red") +
  labs(
    x = NULL, y = "(µg/m3)", title = "Evolución de NO2 en Madrid",
    subtitle = "Concentración por zonas en las estaciones de medición",
    caption = "Fuente: Portal de datos abiertos del Ayuntamiento de Madrid"
  ) +
  theme_minimal() +
  theme(legend.position = "none") +
  facet_wrap(~zona, ncol = 1)

plot_air_mad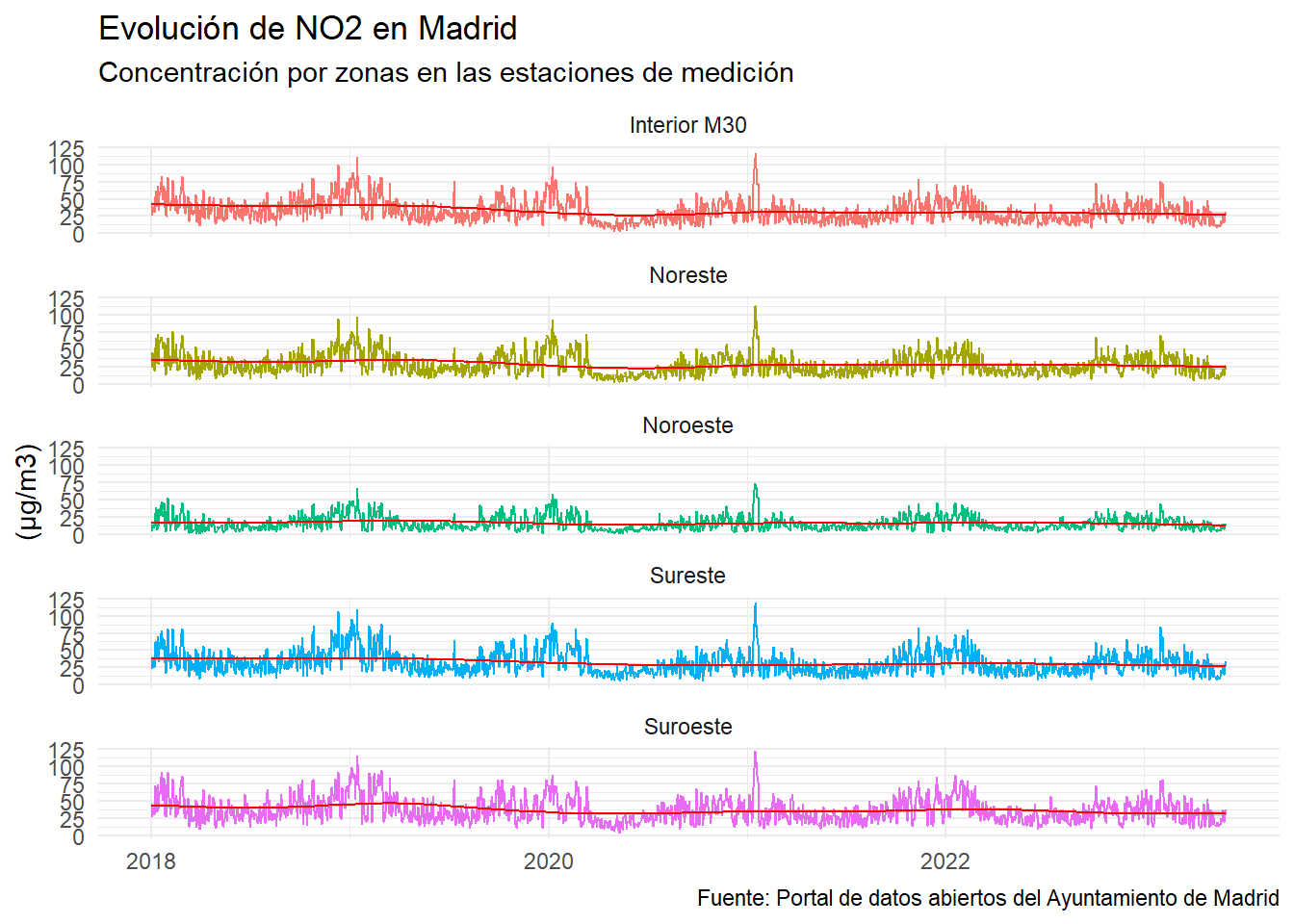

3.3 Preparación de los datos

En esta fase se abordan la limpieza y transformación de los datos de contaminación del aire para su posterior análisis.

En esta sección, se explorarán las técnicas y métodos para limpiar los datos de contaminación del aire y abordar los problemas de calidad, como los valores faltantes, los valores atípicos y los errores de medición. Se describirán las siguientes actividades:

Fase III: limpieza y transformación de los datos de calidad del aire

• Tratamiento de valores faltantes, por averías en las estaciones de monitoreo, por ejemplo. Imputación o eliminación los valores faltantes de manera adecuada.

• Identificar y analizar los valores atípicos en los datos de contaminación del aire, en días de calima, por ejemplo. Evaluar si los valores atípicos son errores de medición o representan información relevante.

• Resolución de errores de medición, si los hubiera.

• Ingeniería de variables: normalización, codificación de variables categóricas, agregación (pasar de frecuencia horaria a frecuencia diaria en la medición delos contaminantes).

Librarías y funciones en R

• Manipulación de datos (valores atípicos y datos faltantes): dplyr
• Manipulación de datos a lo ancho y largo: tidyr

no2 <- air_mad %>% 
  filter(nom_abv == "NO2")

no2 %>% 
  count(V)

# A tibble: 2 × 2
  V         n
  <chr> <int>
1 N       819
2 V     90267

Hay un total de 819 datos no válidos y 90267 válidos. Se seleccionan solamente los datos válidos:

no2 <- no2 %>% 
  filter(V == "V")

3.3.1 Valores faltantes (NA)

¿Existen datos con valores faltantes, codificados como NA (not available)?:

no2 %>%
  count(is.na(valor))

# A tibble: 1 × 2
  `is.na(valor)`     n
  <lgl>          <int>
1 FALSE          90267

No se encuentran valores válidos con NA en el campo valor.

Como parte del proceso de preparación de los datos, a continuación, se agrupan los datos según la variable zona y se genera la variable valor_zona que representa la media por zona y día. Se crea el objeto no2_zona para tal efecto.

no2_zona <- no2 %>% 
  group_by(zona, fecha) %>% 
  summarise(valor_zona = mean(valor, na.rm = T))

3.3.2 Valores atípicos (outliers)

La detección de valores atípicos es fundamental en esta tercera fase. A modo de ejemplo, se ilustra como detectar valores atípicos en la zona Interior de la M30 con el criterio de 1,5 veces el rango intercuartílico.

anomalias <- lapply(unique(no2_zona$zona), function(x) {
  aux_data <- no2_zona %>%
    filter(zona == x) %>%
    select(zona, fecha, valor_zona)
  
  aux_data <- aux_data %>%
    group_by(month(fecha), year(fecha)) %>%
    mutate(anomaly = !between(
      valor_zona,
      quantile(aux_data$valor_zona, probs = c(.25)) - 1.5 * IQR(valor_zona),
      quantile(aux_data$valor_zona, probs = c(.75)) + 1.5 * IQR(valor_zona)
    )) %>% 
    ungroup() %>% 
    select(zona, fecha, anomaly)
})
anomalias <- do.call(rbind, anomalias)
  
no2_zona <- left_join(no2_zona, anomalias, by = c("zona", "fecha"))

no2_zona %>% 
  filter(zona == "Interior M30") %>% 
  ggplot(aes(fecha, valor_zona, color = anomaly)) +
  geom_point() +
  scale_x_date() + 
  scale_color_manual(values = c("black", "red")) +
  labs(title = "Anomalías NO2 por zona de interes",
       subtitle = "Interior M30",
       x = NULL, 
       y = "(µg/m3)") +
  theme_minimal() +
  theme(legend.position = "bottom")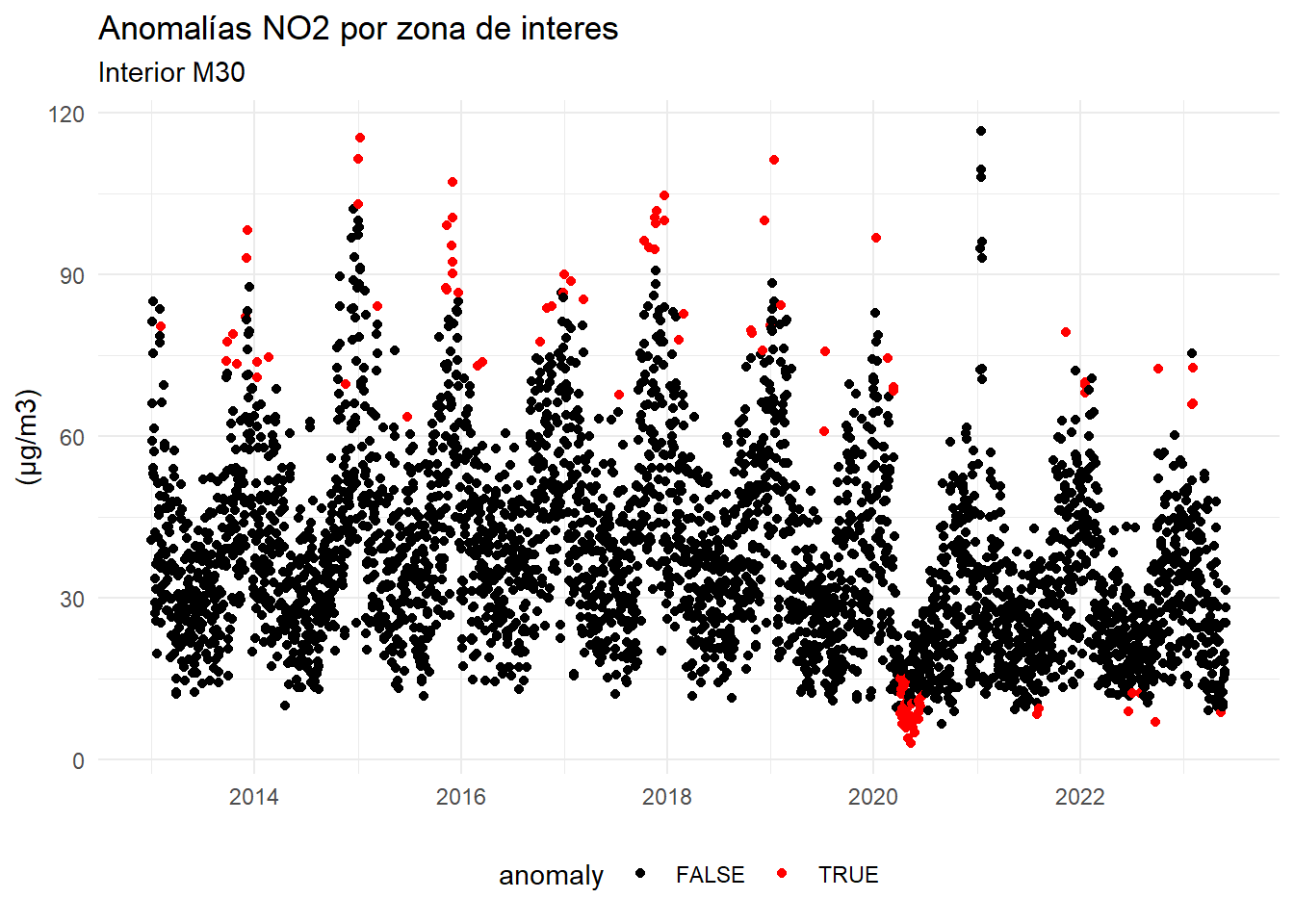

3.3.3 Ingeniería de variables

Una vez se han realizado los ajustes en los datos se procede a creación de variables de interés. De acuerdo con el DECRETO 140/2017, de 21 de noviembre, del Consejo de Gobierno, por el que se aprueba el protocolo marco de actuación durante episodios de alta contaminación por dióxido de nitrógeno (NO2) en la Comunidad de Madrid, el objetivo de la media anual se fija en los 40 µg/m3. En consecuencia, se genera la variable lógica objetivo_anual, que tomará el valor TRUE cuando los valores son inferiores o iguales a 40 µg/m3 del objetivo anual y FALSE en caso contrario.

no2_zona <- no2_zona %>%
  mutate(objetivo_anual = valor_zona <= 40)

no2_zona %>% 
  ggplot(aes(zona, fill = objetivo_anual)) +
  geom_bar(position = "fill") +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Cumplimiento del tope de 40 µg/m3 de NO2",
       subtitle = "porcentaje de cumplimiento por zona",
       x = NULL,
       y = "%", 
       fill = "Cumplimiento del objetivo") +
  theme(legend.position = "bottom")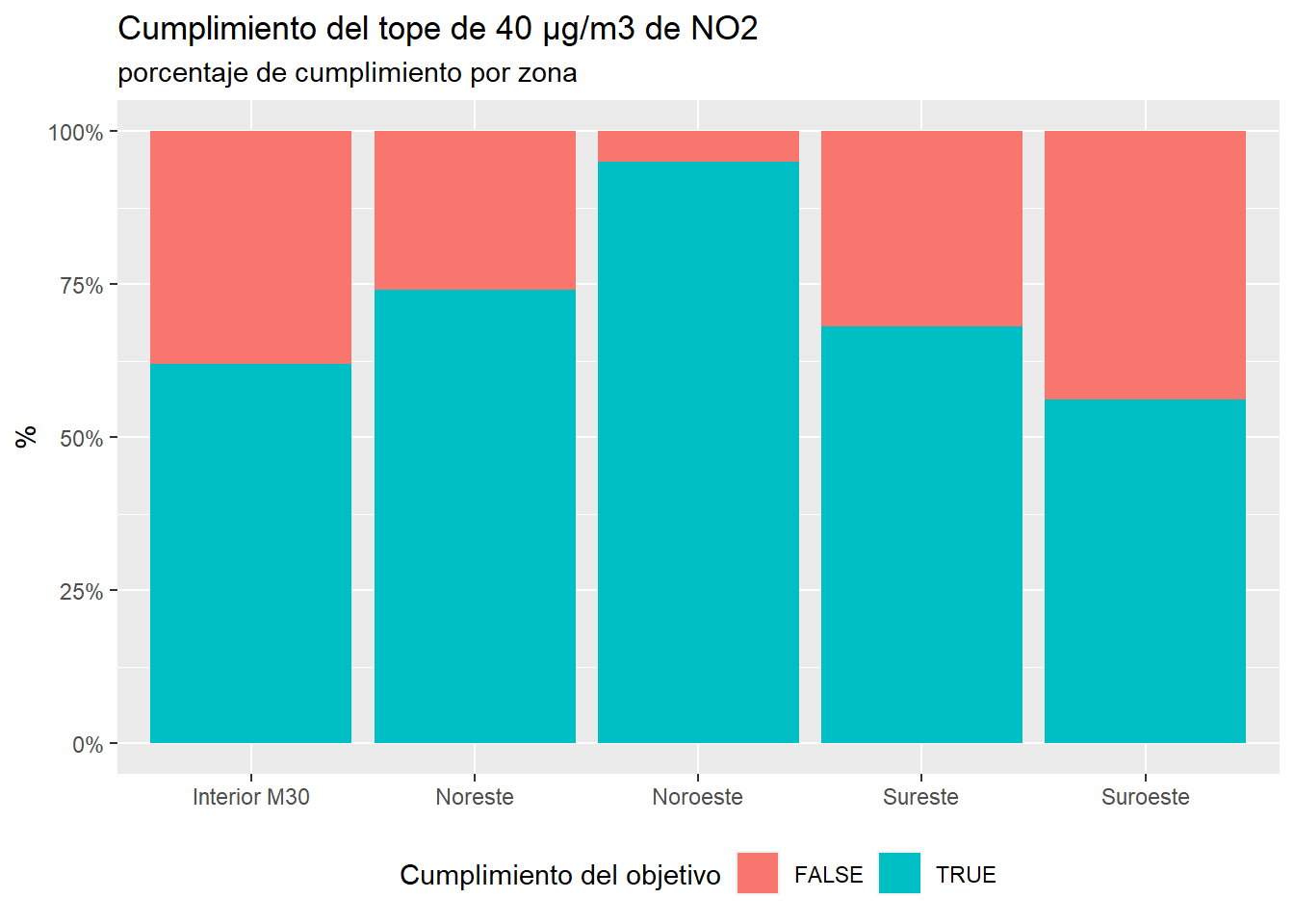

Se observa que la zona que se encuentra más cerca del cumplimiento de los objetivos es la zona Noroeste, mientras la que se encuentra más alejada es la zona Suroeste. En General las zonas del Norte obtienen mejores resultados.

Dado que se trata de un objetivo anual se aplica a cada zona una media móvil con ventana de un año para ver la evolución de los datos:

library(zoo) 
no2_zona <- no2_zona %>% 
  group_by(zona) %>%
  mutate(valor_zona_anual = rollmean(valor_zona, k = 365, fill = NA, align = 'right'))

no2_zona %>% 
  filter(fecha >= "2014-01-01") %>% 
  ggplot(aes(fecha, valor_zona_anual, color = zona)) +
  geom_line() +
  scale_x_date() +
  geom_hline(yintercept = 40, color = "red") +
  labs(title = "Cumplimiento del tope de 40 µg/m3 de NO2",
       subtitle = "media móvil anual por zona",
       x = NULL,
       y = "µg/m3 de NO2", 
       color = "Zona") +
  theme(legend.position = "bottom")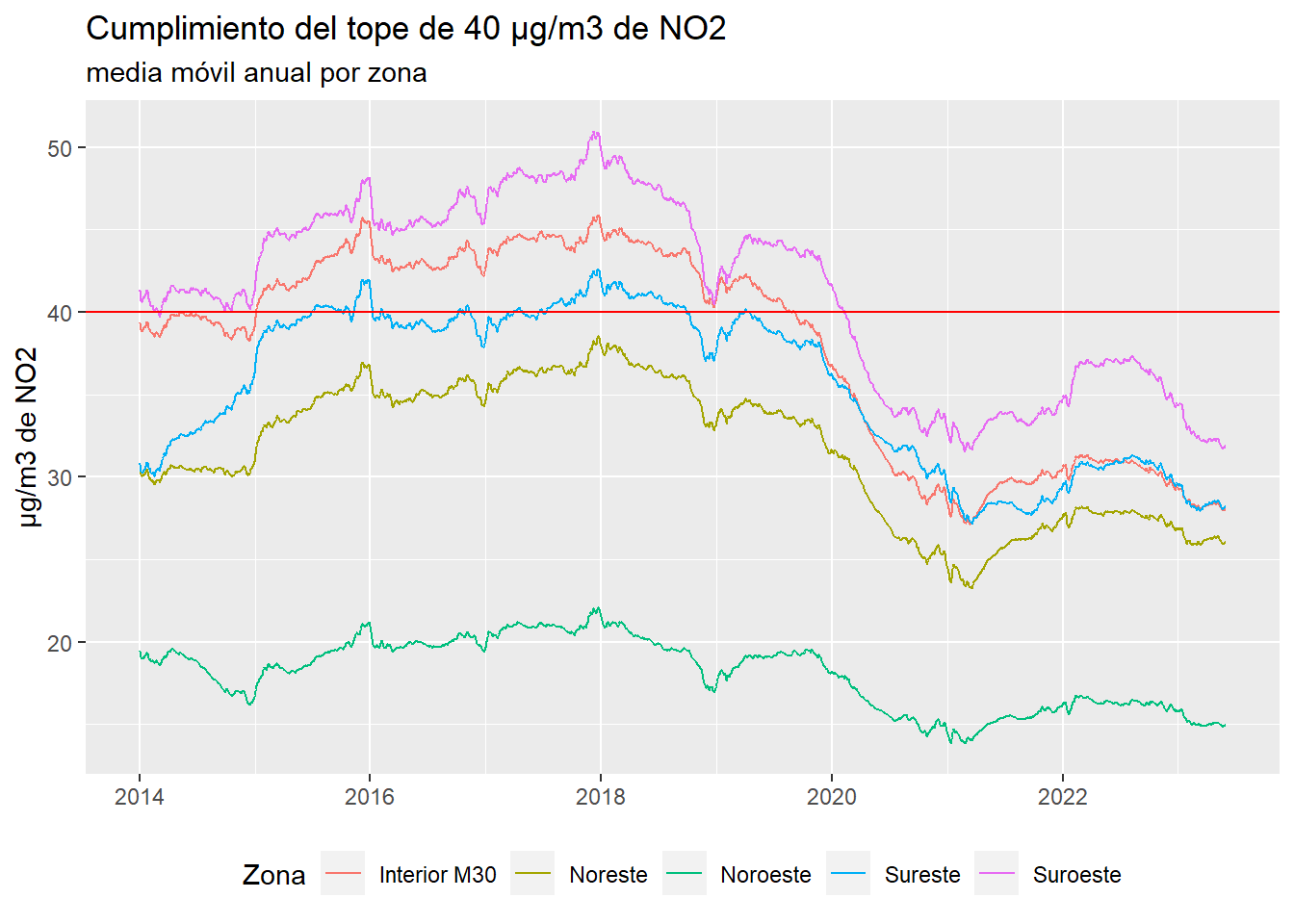

Se observa un claro cambio en los niveles de la contaminación desde 2020, el año del comienzo de la pandemia de COVID-19.

El siguiente paso será centrar el estudio en la zona de calidad del aire con mayores niveles de contaminación, el interior de la M30.

Se filtra la zona de calidad del aire con mayores niveles de contaminación, la zona “Interior M30” y se crea el subconjunto no2_zona_m30.

no2_zona_m30 <- no2_zona %>%
  filter(zona == "Interior M30" & anomaly == FALSE) %>% 
  ungroup() %>% 
  select(fecha, valor_zona)

Se visualizan los datos de NO2 en el interior de la M30

library(timetk)

no2_zona_m30 %>%
  plot_time_series(fecha, valor_zona)

3.3.4 Ingeniería de variables

Se generan una serie de variables útiles para la predicción y se define h como el horizonte de predicción y que indica, también, el número de lags.

• fecha_num: valor numérico normalizado de la fecha.

• dow: valor numérico indicativo del día de la semana (siendo lunes el primer día).

• month: valor numérico indicativo del mes.

• quarter: valor numérico indicativo del trimestre.

• year: año.

La creación de variables auxiliares como día de la semana, mes o año en los modelos de machine learning para la predicción de series temporales es necesaria debido a varias razones:

1. Tendencia estacional: Muchas series temporales exhiben patrones estacionales que se repiten en intervalos regulares, como estacionalidad diaria, mensual o anual. Al incluir variables como día de la semana, mes o año, los modelos de machine learning pueden capturar mejor estos patrones y ajustar las predicciones en consecuencia.

2. Diferenciación de comportamiento: Las series temporales pueden tener diferentes comportamientos dependiendo del día de la semana o el mes. Por ejemplo, las ventas minoristas pueden ser más altas los fines de semana o durante las vacaciones. Al incluir variables auxiliares, los modelos pueden aprender estas diferencias y mejorar la precisión de las predicciones.

3. Cambios estacionales y tendencias a largo plazo: Al considerar variables como el año, los modelos pueden capturar cambios estacionales y tendencias a largo plazo en los datos. Por ejemplo, una serie de tiempo que muestra un crecimiento anual constante puede beneficiarse de la inclusión del año como variable para predecir futuros incrementos.

4. Ajuste a patrones no lineales: Al utilizar variables auxiliares, los modelos de machine learning pueden capturar patrones no lineales en las series temporales. Por ejemplo, puede haber interacciones complejas entre el día de la semana y el mes que influyen en el comportamiento de la serie.

En resumen, la inclusión de variables auxiliares como día de la semana, mes o año en los modelos de machine learning para la predicción de series temporales permite capturar patrones estacionales, diferencias de comportamiento, cambios estacionales y tendencias a largo plazo, así como ajustar a patrones no lineales. Esto mejora la capacidad del modelo para realizar pronósticos precisos y más sólidos en series temporales.

Además de las variables auxiliares mencionadas anteriormente, la inclusión de lags o retardos en los modelos de machine learning para la predicción de series temporales es otra técnica importante. Los lags representan la observación pasada de la serie en diferentes puntos de tiempo y se utilizan como variables predictoras en el modelo.

La inclusión de lags permite capturar la dependencia temporal en los datos. Las observaciones pasadas de la serie pueden contener información relevante para predecir el valor futuro. Al incluir lags en el modelo, se proporciona al algoritmo de machine learning información sobre cómo las observaciones anteriores afectan a las futuras.

La elección adecuada de los lags es importante. Dependerá de la naturaleza de la serie y de su periodicidad. Por ejemplo, en una serie de tiempo mensual, se pueden incluir lags correspondientes a los meses anteriores. En una serie de tiempo diaria, se pueden considerar lags que representen los días anteriores.

En el caso de los modelos seleccionados se aplica lags de 1 al 14 por medio de la función lag_transformer() creada en el chunk siguiente.

En definitiva inclusión de lags permite al modelo capturar patrones de autocorrelación y estacionalidad en la serie temporal. Además, puede ayudar a capturar cambios en la dinámica de la serie y a mejorar la precisión de las predicciones.

Autocorrelación y estacionalidad

La autocorrelación temporal se refiere a la correlación entre una observación y sus observaciones pasadas a lo largo del tiempo. Es una medida que indica cómo una observación en un momento dado está relacionada con las observaciones anteriores en la misma serie (Shumway and Stoffer 2017). Se trata un concepto fundamental en el análisis de series temporales, ya que proporciona información sobre la dependencia temporal y los patrones de comportamiento en los datos. Permite identificar si hay una relación lineal o no lineal entre las observaciones pasadas y presentes.

La estacionalidad se refiere a patrones regulares y repetitivos que se observan en los datos a lo largo del tiempo. Estos patrones pueden ser de corto plazo, como fluctuaciones diarias o semanales, o de largo plazo, como fluctuaciones estacionales o anuales (Hyndman 2021). Se trata de una característica común en muchos tipos de datos, como las ventas minoristas, la demanda de productos, el tráfico web, el clima y muchos otros.

Sin embargo, es importante tener en cuenta que la inclusión de demasiados lags puede aumentar la complejidad del modelo y llevar a problemas de sobreajuste¹. Por lo tanto, se debe encontrar un equilibrio adecuado al seleccionar los lags relevantes y evitar la inclusión de lags redundantes.

Para mitigasr los problemas de sobreajuste existen varias técnicas como:

• Regularización: Se aplica una penalización a los coeficientes o parámetros del modelo para evitar que tomen valores extremos.
• Validación cruzada: Se divide el conjunto de datos en subconjuntos de entrenamiento y validación para evaluar el rendimiento del modelo en datos no vistos durante el entrenamiento.
• Reducción de la complejidad del modelo: Se puede reducir el número de características o la complejidad del modelo para evitar un ajuste excesivo.
• Recopilación de más datos: Obtener más datos puede ayudar a reducir el sobreajuste al proporcionar una visión más completa y representativa del problema.

En el caso de este proyecto se aplica el ajuste de parámetros y validación cruzada.

# el horizonte
h <- 21

# función auxilar para hacer los lags
lag_transformer <- function(data){
  data %>%
    tk_augment_lags(valor_zona, .lags = 1:14) %>%
    ungroup()
}

# Extensión de los datos en h
no2_zona_m30_ext <- no2_zona_m30 %>%
  future_frame(
    .date_var = "fecha", 
    .length_out = h,
    .bind_data  = TRUE
  ) %>%
  ungroup()

# Generación de variables
no2_zona_m30_ext <- no2_zona_m30_ext %>% 
  mutate(
    fecha_num = normalize_vec(as.numeric(fecha)),
    dow = wday(fecha, week_start = 1), 
    month = month(fecha),
    quarter = quarter(fecha),
    year = year(fecha)
  ) %>%
  ungroup()

# Añadir lags
no2_zona_m30_ext <- no2_zona_m30_ext %>%
  lag_transformer()

3.3.5 División del dataset (entrenamamineto-validación y predicción)

A continuación se divide el conjunto de datos en dos subconjuntos: uno para el entrenamiento y validación y otro para la predicción.

# Datos de entrenamiento
train_data <- no2_zona_m30_ext %>%
  drop_na()

# Datos para la prediccción
future_data <- no2_zona_m30_ext %>%
  filter(is.na(valor_zona))

Los datos para el entrenamiento.

str(train_data)

tibble [3,674 × 21] (S3: tbl_df/tbl/data.frame)
 $ fecha           : Date[1:3674], format: "2013-01-15" "2013-01-16" ...
 $ valor_zona      : num [1:3674] 33.6 31.6 36.2 25.7 28.3 ...
 $ fecha_num       : num [1:3674] 0.00366 0.00392 0.00419 0.00445 0.00471 ...
 $ dow             : num [1:3674] 2 3 4 5 6 7 1 2 3 4 ...
 $ month           : num [1:3674] 1 1 1 1 1 1 1 1 1 1 ...
 $ quarter         : int [1:3674] 1 1 1 1 1 1 1 1 1 1 ...
 $ year            : num [1:3674] 2013 2013 2013 2013 2013 ...
 $ valor_zona_lag1 : num [1:3674] 42.2 33.6 31.6 36.2 25.7 ...
 $ valor_zona_lag2 : num [1:3674] 27.2 42.2 33.6 31.6 36.2 ...
 $ valor_zona_lag3 : num [1:3674] 29.2 27.2 42.2 33.6 31.6 ...
 $ valor_zona_lag4 : num [1:3674] 57.2 29.2 27.2 42.2 33.6 31.6 36.2 25.7 28.3 19.7 ...
 $ valor_zona_lag5 : num [1:3674] 61.5 57.2 29.2 27.2 42.2 33.6 31.6 36.2 25.7 28.3 ...
 $ valor_zona_lag6 : num [1:3674] 52.5 61.5 57.2 29.2 27.2 42.2 33.6 31.6 36.2 25.7 ...
 $ valor_zona_lag7 : num [1:3674] 54.2 52.5 61.5 57.2 29.2 27.2 42.2 33.6 31.6 36.2 ...
 $ valor_zona_lag8 : num [1:3674] 53.1 54.2 52.5 61.5 57.2 29.2 27.2 42.2 33.6 31.6 ...
 $ valor_zona_lag9 : num [1:3674] 75.4 53.1 54.2 52.5 61.5 57.2 29.2 27.2 42.2 33.6 ...
 $ valor_zona_lag10: num [1:3674] 85 75.4 53.1 54.2 52.5 61.5 57.2 29.2 27.2 42.2 ...
 $ valor_zona_lag11: num [1:3674] 81.2 85 75.4 53.1 54.2 52.5 61.5 57.2 29.2 27.2 ...
 $ valor_zona_lag12: num [1:3674] 66.1 81.2 85 75.4 53.1 54.2 52.5 61.5 57.2 29.2 ...
 $ valor_zona_lag13: num [1:3674] 59.1 66.1 81.2 85 75.4 53.1 54.2 52.5 61.5 57.2 ...
 $ valor_zona_lag14: num [1:3674] 40.7 59.1 66.1 81.2 85 75.4 53.1 54.2 52.5 61.5 ...

Los datos para la predicción:

str(future_data)

tibble [21 × 21] (S3: tbl_df/tbl/data.frame)
 $ fecha           : Date[1:21], format: "2023-06-01" "2023-06-02" ...
 $ valor_zona      : num [1:21] NA NA NA NA NA NA NA NA NA NA ...
 $ fecha_num       : num [1:21] 0.995 0.995 0.995 0.996 0.996 ...
 $ dow             : num [1:21] 4 5 6 7 1 2 3 4 5 6 ...
 $ month           : num [1:21] 6 6 6 6 6 6 6 6 6 6 ...
 $ quarter         : int [1:21] 2 2 2 2 2 2 2 2 2 2 ...
 $ year            : num [1:21] 2023 2023 2023 2023 2023 ...
 $ valor_zona_lag1 : num [1:21] 25.3 NA NA NA NA NA NA NA NA NA ...
 $ valor_zona_lag2 : num [1:21] 31.5 25.3 NA NA NA NA NA NA NA NA ...
 $ valor_zona_lag3 : num [1:21] 28.2 31.5 25.3 NA NA NA NA NA NA NA ...
 $ valor_zona_lag4 : num [1:21] 15.9 28.2 31.5 25.3 NA NA NA NA NA NA ...
 $ valor_zona_lag5 : num [1:21] 16.4 15.9 28.2 31.5 25.3 NA NA NA NA NA ...
 $ valor_zona_lag6 : num [1:21] 19.6 16.4 15.9 28.2 31.5 25.3 NA NA NA NA ...
 $ valor_zona_lag7 : num [1:21] 25.4 19.6 16.4 15.9 28.2 31.5 25.3 NA NA NA ...
 $ valor_zona_lag8 : num [1:21] 18.3 25.4 19.6 16.4 15.9 28.2 31.5 25.3 NA NA ...
 $ valor_zona_lag9 : num [1:21] 15.1 18.3 25.4 19.6 16.4 15.9 28.2 31.5 25.3 NA ...
 $ valor_zona_lag10: num [1:21] 18.2 15.1 18.3 25.4 19.6 16.4 15.9 28.2 31.5 25.3 ...
 $ valor_zona_lag11: num [1:21] 10.5 18.2 15.1 18.3 25.4 19.6 16.4 15.9 28.2 31.5 ...
 $ valor_zona_lag12: num [1:21] 9.9 10.5 18.2 15.1 18.3 25.4 19.6 16.4 15.9 28.2 ...
 $ valor_zona_lag13: num [1:21] 12.5 9.9 10.5 18.2 15.1 18.3 25.4 19.6 16.4 15.9 ...
 $ valor_zona_lag14: num [1:21] 10.7 12.5 9.9 10.5 18.2 15.1 18.3 25.4 19.6 16.4 ...

3.3.6 Validación cruzada para evaluación de los modelos

La librería timek con la función time_series_cv() crea conjuntos de validación cruzada de rsample para series temporales. Esta función genera un plan de muestreo comenzando con las observaciones más recientes de la serie temporal y avanzando hacia atrás. El procedimiento de muestreo es similar a rsample::rolling_origin(), pero se enfoca en los datos más recientes de la serie temporal para la validación cruzada.

Es por ello, que el conjunto de datos de entrenamiento se refiere a la serie completa conocida ya que internamente va a dividir los datos en varias partes con sus subconjuntos de entrenamiento y test.

resamples_tscv <- time_series_cv(
  data        = train_data,
  assess      = h,
  initial     = 12 * 4 * h,
  skip        = 12 * 3 * h,
  slice_limit = 4
)

resamples_tscv

# Time Series Cross Validation Plan 
# A tibble: 4 × 2
  splits            id    
  <list>            <chr> 
1 <split [1008/21]> Slice1
2 <split [1008/21]> Slice2
3 <split [1008/21]> Slice3
4 <split [1008/21]> Slice4

Note

La validación cruzada es una técnica utilizada en el análisis de series de tiempo para evaluar la estabilidad de los modelos a lo largo del tiempo. Consiste en dividir los datos de la serie de tiempo en diferentes subconjuntos, aplicar un modelo predictivo a cada subconjunto y luego comparar las predicciones generadas por cada modelo. Es importante por varias razones:

1. Evalúa la estabilidad del modelo.

2. Valida el rendimiento del modelo

3. Permite la comparación de modelos.

En el gráfico inferior se observa cómo se generó la división de los datos para la validación cruzada. En color azul se muestra la parte de entrenamiento y en rojo la del test. Posteriormente los modelos seleccionados se aplicarán a cada trozo de entrenamiento por separado y gracias a la parte del test se generarán las estadísticas que evaluarán los modelos en cada trozo. De esta forma, se obtendrán 4 estadísticas de rendimiento de cada modelo, lo que ayudará a no caer en el sobreajuste.

resamples_tscv %>%
  tk_time_series_cv_plan() %>%
  plot_time_series_cv_plan(fecha, valor_zona, .facet_ncol = 2, .interactive = FALSE)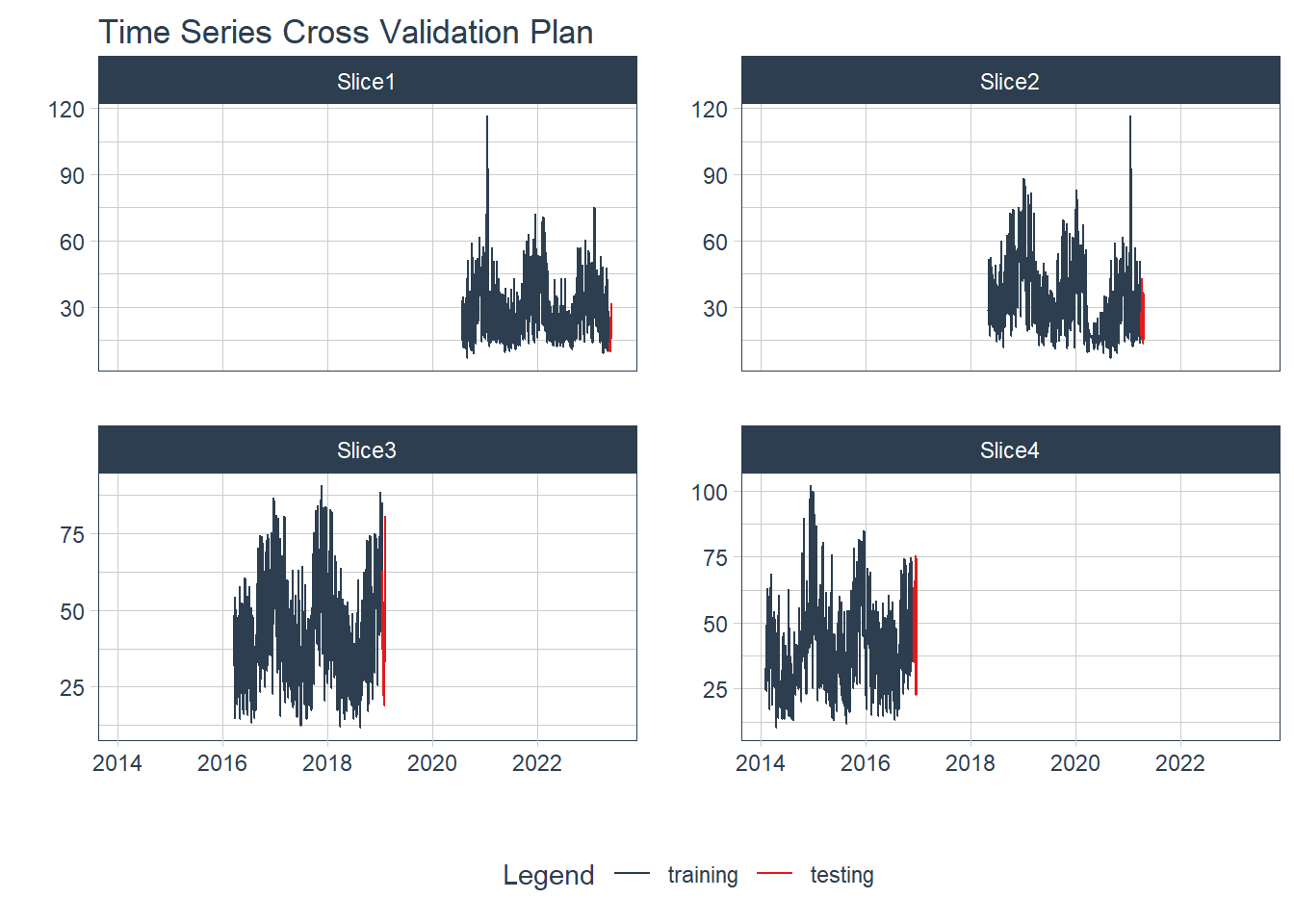

3.4 Modelado

Fase IV: selección de técnicas de modelado

• Objetivos del análisis: identificar si el objetivo es la predicción, clasificación, agrupación u otra tarea específica.

• Naturaleza de los datos: evaluar la estructura de los datos, la presencia de variables dependientes e independientes, y si se trata de datos espaciales, temporales, etc.

• Disponibilidad de datos: considerar la cantidad y calidad de los datos disponibles, así como los recursos computacionales y el tiempo requerido para entrenar los modelos.

• Conocimiento del dominio: utilizar el conocimiento experto en contaminación del aire para seleccionar técnicas relevantes y realizar ajustes apropiados.

Librerías y funciones en R

Tidymodeling + tidymodels + modeltime + modeltime.resample

Base Models + earth + glmnet + xgboost + lightgbm

Core Packages + tidyverse + lubridate + timetk
+ bonsai

set.seed(160191)

Proceso de modelado en ciencia de datos

El principal paquete que se utilzará en el modelado de los datos es el paquete modeltime de R, apropiado para series temporales como es la distribución del NO2 durante 10 años con mediciones diarias. modeltime ofrece una variedad de herramientas y técnicas avanzadas para el pronóstico de series temporales. Está diseñado para simplificar el proceso de construcción, evaluación y despliegue de modelos de series temporales.

Con modeltime, los usuarios pueden realizar tareas como la selección automática de modelos, la construcción de modelos en paralelo, la agregación de modelos, la validación cruzada y la generación de pronósticos. También ofrece una interfaz intuitiva para ajustar y personalizar modelos de series temporales, lo que facilita su adaptación a diferentes escenarios. Además, permite la integración con otras bibliotecas populares de R, como tidyverse, lo que brinda un enfoque coherente para el preprocesamiento de datos y el análisis exploratorio.

Para más información sobre la biblioteca véase la documentación oficial en sobre modeltime.

# Tidymodeling
library(tidymodels)
library(modeltime)
library(modeltime.resample)

# Base Models
library(earth)
library(glmnet)
library(xgboost)
library(lightgbm)

# Core Packages
library(tidyverse)
library(lubridate)
#library(timetk)
library(bonsai)


set.seed(160191)

3.4.1 La “receta” del modelo

El paquete recipes nace de la analogía entre preparar una receta de cocina y preprocesar los datos (como si de una receta de libro de cocina se tratase) y el cocinado (modelado).

Se crea la receta del modelo, siendo la variable dependiente valor_zona y los predictores el resto de valiables del dataset.

#library(recipes)
recipe_spec <- recipe(valor_zona ~ ., train_data)

# recipe_spec <- recipe(valor_zona ~ fecha_num + dow + month + quarter +  year + valor_zona_lag1 + valor_zona_lag2 + ... valor_zona_lag21", train_data)

3.4.2 Modelos propuestos

📉 Modelo 1: Generalized Linear Model with Elastic Net regularization (GLMNET): es una técnica de modelado que combina la regresión lineal generalizada con la regularización elastic net.

GLMNET es útil cuando se trabaja con conjuntos de datos con un gran número de variables predictoras, ya que ayuda a seleccionar y ajustar las variables más relevantes. GLMNET utiliza una combinación de la regularización L1 (LASSO) y L2 (Ridge) para penalizar los coeficientes de las variables y controlar la complejidad del modelo. Esto permite seleccionar automáticamente las variables más relevantes y reducir la tendencia al sobreajuste. Por ejemplo, supongamos que se desea predecir el precio de la vivienda en función de múltiples variables, como el tamaño, el número de habitaciones, la ubicación, etc. Aplicando GLMNET, se identifican las variables más importantes para predecir el precio y ajustar el modelo de regresión lineal generalizada al mismo tiempo.

En el caso NO2 se procede con la siguiente especificación:

# Especificación
model_spec_glmnet <- linear_reg(penalty = 0.04) %>%
  set_engine("glmnet")

# Ajuste
workflow_fit_glmnet <- workflow() %>%
  add_model(model_spec_glmnet) %>%
  add_recipe(recipe_spec %>% step_rm(fecha)) %>%
  fit(train_data) %>%
    recursive(
      transform  = lag_transformer,
      train_tail = tail(train_data, h))

Note

Nótese que cuando se determina el workflow del modelo se desestima la variable fecha aplicando una modificación en la receta: add_recipe(recipe_spec %>% step_rm(fecha))

Esto es debido a que el modelo no soporta variables en formato de fecha (Date).

📊 Modelo 2: Multivariate Adaptive Regression Splines (MARS). es una técnica de modelado que utiliza funciones de base para aproximar relaciones no lineales entre variables predictoras y una variable objetivo. Se adapta a los datos mediante la construcción de una red de segmentos de regresión que capturan cambios en la relación entre las variables.

Por ejemplo, supongamos que queremos predecir el precio de una vivienda en función de variables como el tamaño, el número de habitaciones y la ubicación. Al aplicar el modelo MARS, éste identificará los segmentos de regresión óptimos para cada variable y construirá un modelo no lineal que se ajuste mejor a los datos. Esto permite capturar relaciones complejas y no lineales entre las variables predictoras y la variable objetivo.

Este tipo de modelos también puede aplicarse para la modelización de la calidad de aire. García Nieto and Álvarez Antón (2014) modelizó la calidad del aire de Gijón con el modelo MARS. El estudio explora el uso de este algoritmo de regresión no paramétrico que puede aproximar la relación entre las variables de entrada y salida y expresarla matemáticamente. Se recopiló un conjunto de datos experimental de contaminantes del aire peligrosos durante tres años (2006-2008) y se utilizó para crear un modelo altamente no lineal de la calidad del aire en el área urbana de Gijón basado en la técnica de MARS.

En el caso NO2 se procede con la siguiente especificación:

# Especificación
model_spec_mars <- mars(mode = "regression") %>%
  set_engine("earth")

# Ajuste
workflow_fit_mars <- workflow() %>%
  add_model(model_spec_mars) %>%
  add_recipe(recipe_spec) %>%
  fit(train_data) %>%
    recursive(
      transform  = lag_transformer,
      train_tail = tail(train_data, h))

📉 Modelo 3: LightGBM: es un modelo de aprendizaje automático basado en árboles de decisión que se destaca por su eficiencia y velocidad en el procesamiento de grandes volúmenes de datos. Utiliza el algoritmo de refuerzo (boosting) para construir una serie de árboles de decisión que se combinan para mejorar la precisión de las predicciones.

Una de las principales características de LightGBM es su capacidad para manejar datos con alta dimensionalidad y realizar una selección automática de características importantes. También utiliza un enfoque de partición de datos basado en hojas, lo que permite una mayor eficiencia en el proceso de entrenamiento.

Un ejemplo de aplicación de LightGBM puede ser en la predicción de la satisfacción del cliente en una empresa de comercio electrónico. Se pueden utilizar características como el historial de compras, el tiempo de respuesta del servicio al cliente y la interacción en redes sociales para predecir la satisfacción del cliente. Al entrenar un modelo LightGBM con estos datos, se puede obtener un modelo eficiente y preciso que permita identificar patrones y factores clave que influyen en la satisfacción del cliente.

En el caso NO2 se procede con la siguiente especificación:

# Especificación
model_spec_lightgbm <- boost_tree(mode = "regression",
                                  trees = 400,
                                  learn_rate = 0.008,
                                  tree_depth = 12,
                                  min_n = 50) %>%
  set_engine("lightgbm")

# Ajuste
workflow_fit_lightgbm <- workflow() %>%
  add_model(model_spec_lightgbm) %>%
  add_recipe(recipe_spec %>% step_rm(fecha)) %>%
  fit(train_data) %>%
    recursive(
      transform  = lag_transformer,
      train_tail = tail(train_data, h))

Note

Nótese que cuando se determina el workflow del modelo se desestima la variable fecha aplicando una modificación en la receta: add_recipe(recipe_spec %>% step_rm(fecha))

Esto es debido a que el modelo no soporta variables en formato de fecha (Date).

📊 Modelo 4: Prophet boost con crecimiento logarítmico: es una herramienta de predicción de series temporales desarrollada por Facebook. Al especificar un crecimiento logarítmico en Prophet, se asume que la tasa de crecimiento de la serie temporal disminuye con el tiempo. Esto es útil cuando los datos muestran un crecimiento inicial rápido seguido de una desaceleración.

Por ejemplo, supongamos que deseamos predecir las ventas de un producto a lo largo del tiempo. Si aplicamos el modelo Prophet con crecimiento logarítmico, capturará la tendencia de crecimiento inicial acelerado y luego la desaceleración esperada. Esto puede ser útil para ajustar mejor la serie temporal y realizar pronósticos más precisos.

El modelo Prophet también se utiliza en la predicción del la contaminación del aire. Un ejemplo es la predicción de la contaminación en Seúl (Shen, Valagolam, and McCalla 2020). El modelo logró predecir con precisión la concentración de varios contaminantes hasta un año de antelación, superando a otros modelos similares.

En el caso NO2 se procede con la siguiente especificación:

# Especificación
model_spec_prophet_boost_log <- prophet_boost(
  mode = 'regression',
  growth = 'linear',
  seasonality_yearly = T,
  seasonality_weekly = T,
  seasonality_daily = F,
  logistic_floor = min(train_data$valor_zona),
  logistic_cap = max(train_data$valor_zona),
  changepoint_num = .8,
  learn_rate = .001,
  tree_depth = 4,
  trees = 2000
) %>%
  set_engine("prophet_xgboost")

# Ajuste
workflow_fit_prophet_boost_log <- workflow() %>%
  add_model(model_spec_prophet_boost_log) %>%
  add_recipe(recipe_spec %>% step_rm(fecha_num, dow, month, quarter, year)) %>%
  fit(train_data) %>%
    recursive(
      transform  = lag_transformer,
      train_tail = tail(train_data, h))

Note

Nótese que cuando se determina el workflow del modelo se desestima la variable fecha_num, dow, month, quarter, year aplicando una modificación en la receta: add_recipe(recipe_spec %>% step_rm(fecha_num, dow, month, quarter, year))

Esto se debe a que el modelo Prophet boost con crecimiento logarítmico ya incluye en su estrucura variables que determinan la estacionalidad de los datos como: seasonality_yearly = T o seasonality_weekly = T.

El siguiente paso es agregar cada uno de los modelos a una tabla de Modeltime utilizando modeltime_table().

models_tbl <- modeltime_table(
  workflow_fit_glmnet,
  workflow_fit_mars,
  workflow_fit_lightgbm,
  workflow_fit_prophet_boost_log
)

models_tbl

# Modeltime Table
# A tibble: 4 × 3
  .model_id .model     .model_desc                        
      <int> <list>     <chr>                              
1         1 <workflow> RECURSIVE GLMNET                   
2         2 <workflow> RECURSIVE EARTH                    
3         3 <workflow> RECURSIVE LIGHTGBM                 
4         4 <workflow> RECURSIVE PROPHET W/ XGBOOST ERRORS

Por último, se realizan las predicciones entrenando los modelos seleccionados para los 4 trozos de datos del plan de validación cruzada con el fin de poder comparar los datos de predicción con los datos reales y obtener una buena evaluación de los modelos propuestos.

resamples_fitted <- models_tbl %>%
  modeltime_fit_resamples(
    resamples = resamples_tscv,
    control   = control_resamples(verbose = FALSE)
  )

resamples_fitted

# Modeltime Table
# A tibble: 4 × 4
  .model_id .model     .model_desc                         .resample_results
      <int> <list>     <chr>                               <list>           
1         1 <workflow> RECURSIVE GLMNET                    <rsmp[+]>        
2         2 <workflow> RECURSIVE EARTH                     <rsmp[+]>        
3         3 <workflow> RECURSIVE LIGHTGBM                  <rsmp[+]>        
4         4 <workflow> RECURSIVE PROPHET W/ XGBOOST ERRORS <rsmp[+]>        

3.5 Evaluación

Fase V: Métricas de evaluación de modelos

• MAE (Mean Absolute Error): Es la media de las diferencias absolutas entre las predicciones y los valores reales. Un valor más bajo de MAE indica un mejor ajuste del modelo.

• MAPE (Mean Absolute Percentage Error): Es la media de los porcentajes absolutos de error entre las predicciones y los valores reales. Un valor más bajo de MAPE indica una mayor precisión en las predicciones.

• MASE (Mean Absolute Scaled Error): Es una métrica que compara el error absoluto promedio del modelo con el error absoluto promedio de un modelo ingenuo, generalmente un modelo de caminata aleatoria. Un valor de MASE inferior a 1 indica que el modelo es mejor que el modelo de referencia.

• SMAPE (Symmetric Mean Absolute Percentage Error): Es similar al MAPE, pero utiliza el promedio simétrico de los porcentajes absolutos de error entre las predicciones y los valores reales. Un valor bajo de SMAPE indica una mayor precisión en las predicciones.

• RMSE (Root Mean Squared Error): Es la raíz cuadrada de la media de los errores al cuadrado entre las predicciones y los valores reales. Un valor más bajo de RMSE indica una menor dispersión y un mejor ajuste del modelo.

• RSQ (R-squared): También conocido como coeficiente de determinación, es una medida que indica la proporción de la variabilidad de la variable de respuesta que puede explicar el modelo. Un valor más alto de RSQ indica un mejor ajuste del modelo a los datos observados.

En el campo de la ciencia de datos, la evaluación de modelos es fundamental para garantizar la calidad y el rendimiento de los modelos utilizados. A medida que los datos se vuelven cada vez más complejos y abundantes, los modelos de machine learning se han convertido en una herramienta poderosa para extraer información y tomar decisiones basadas en datos.

La evaluación de modelos de machine learning permite determinar la precisión, la eficacia y la capacidad de generalización de un modelo en función de los datos utilizados. Es crucial evaluar los modelos de forma adecuada para evitar problemas como el sobreajuste (overfitting) o el subajuste (underfitting) y para identificar cualquier sesgo o error en los resultados.

Además, la evaluación de modelos proporciona información valiosa sobre la robustez y la confiabilidad de un modelo en diferentes escenarios y conjuntos de datos. Permite comparar diferentes modelos y enfoques, seleccionar el mejor modelo para una tarea específica y realizar mejoras iterativas para optimizar el rendimiento.

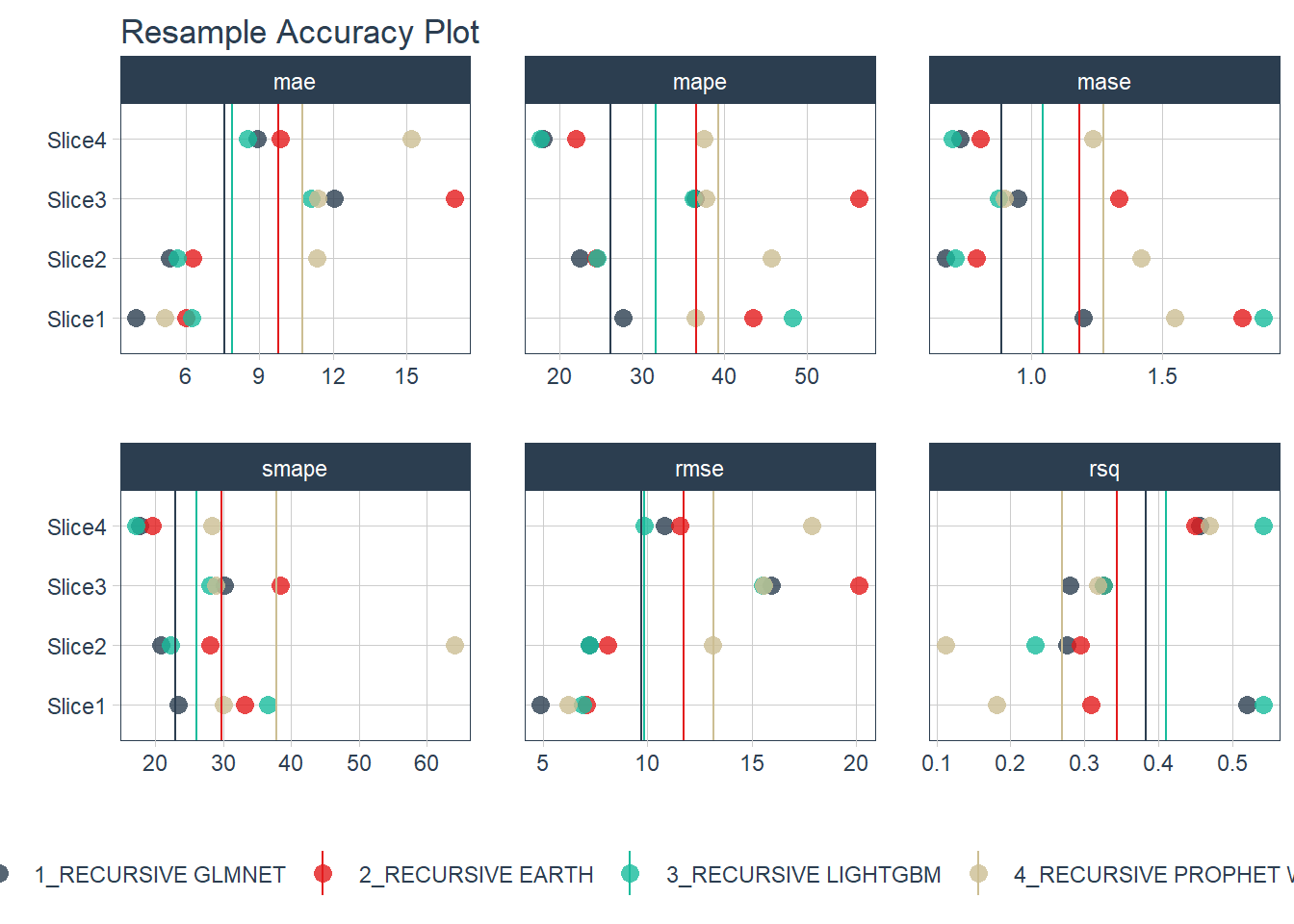
Evaluación de la precisión:

resamples_fitted %>%
    plot_modeltime_resamples(
      .point_size  = 3, 
      .point_alpha = 0.8,
      .interactive = FALSE
    )

resamples_fitted %>%
    modeltime_resample_accuracy(summary_fns = mean) %>%
    table_modeltime_accuracy(.interactive = FALSE)

Accuracy Table
.model_id	.model_desc	.type	n	mae	mape	mase	smape	rmse	rsq
1	RECURSIVE GLMNET	Resamples	4	7.57	26.16	0.88	23.00	9.71	0.38
2	RECURSIVE EARTH	Resamples	4	9.78	36.55	1.18	29.75	11.73	0.34
3	RECURSIVE LIGHTGBM	Resamples	4	7.90	31.70	1.04	26.01	9.87	0.41
4	RECURSIVE PROPHET W/ XGBOOST ERRORS	Resamples	4	10.77	39.32	1.27	37.83	13.19	0.27

Los tres primeros modelos parecen los que mejor se ajustan a los datos. Sin embargo todos los modelos presentan unas métricas con un MAPE bastante elevado. EN este punto habría que reconsiderar la inclusión de más regresores.

El modelo con las métricas más bajas de error es el GLMNET.

Una vez seleccionado el modelo, el siguiente paso deseado sería la predicción a futuro del valor del NO2.

workflow_fit_lightgbm %>% 
  modeltime_table() %>%
  modeltime_forecast(
    new_data    = future_data,
    actual_data = no2_zona_m30_ext,
    keep_data   = TRUE
  ) %>%
  filter(fecha >= "2023-01-01") %>% 
  plot_modeltime_forecast(
    .conf_interval_show = FALSE
  )

3.6 Despliegue

Despliegue de resultados

Presentación de los resultados del análisis de manera clara y comprensible.

• Creación de una ShinyApp: se puede construir una aplicación interactiva que permita a los usuarios explorar y visualizar los datos de contaminación del aire, así como interactuar con los modelos y los resultados obtenidos.

• Implementación de un bot de Twitter: es posible desarrollar un bot de Twitter (rtweet, por ejemplo) que publique actualizaciones y resultados relacionados con la contaminación del aire, lo que permite difundir la información de manera efectiva.

• Comunicación de los hallazgos y recomendaciones: Utilizando RMarkdown y RStudio, se pueden crear informes reproducibles que combinen el código, los resultados y las visualizaciones en un documento HTML, PDF u otro formato, lo que facilita la comunicación y la presentación de los hallazgos del análisis.

Librarías y funciones en R

• shyni

• flexdasboard

Ejemplo de creación de una 📺 ShinyApp en R:

# Carga de la librería shiny
library(shiny)

# Definición de la interfaz de la ShinyApp
ui <- fluidPage(
  titlePanel("Análisis de Contaminación del Aire"),
  sidebarLayout(
    sidebarPanel(
      # Aquí se pueden agregar controles para interactuar con los datos y modelos
    ),
    mainPanel(
      # Aquí se pueden mostrar las visualizaciones y los resultados obtenidos
    )
  )
)

# Definición de la lógica de la ShinyApp
server <- function(input, output) {
  # Aquí se puede incluir el código para cargar los datos, entrenar modelos, etc.
}

# Creación de la ShinyApp
shinyApp(ui = ui, server = server)

La etapa de “Implementación” es el sexto y último paso en el proceso de CRISP-DM. En esta etapa, debemos implementar el modelo seleccionado y seguir sus resultados. Esto puede incluir la generación de informes y visualizaciones para comunicar los resultados del análisis.

En el caso de un análisis de datos sobre la contaminación del aire utilizando R, podríamos utilizar diferentes técnicas para implementar y comunicar los resultados de nuestros modelos. Por ejemplo, si hemos ajustado un modelo de regresión, podríamos utilizar funciones como predict para generar predicciones con nuestro modelo y librerías como ggplot2 para visualizar los resultados. Por ejemplo:

predicciones <- predict(modelo, newdata = datos_test)
datos_test$predicciones <- predicciones

ggplot(datos_test, aes(x = fecha, y = contaminacion)) +
  geom_point() +
  geom_line(aes(y = predicciones), color = "red")

Si hemos ajustado un modelo de series temporales, podríamos utilizar funciones como forecast para generar predicciones con nuestro modelo y librerías como ggplot2 para visualizar los resultados. Por ejemplo:

predicciones <- forecast(modelo, h = length(datos_test$contaminacion))
datos_test$predicciones <- predicciones$mean

ggplot(datos_test, aes(x = fecha, y = contaminacion)) +
  geom_point() +
  geom_line(aes(y = predicciones), color = "red")

También podemos generar informes y visualizaciones para comunicar los resultados de nuestro análisis a otras personas. Por ejemplo, podríamos utilizar librerías como rmarkdown o shiny para crear informes dinámicos o aplicaciones interactivas que muestren los resultados de nuestro análisis.

García Nieto, P. J., and J. C. Álvarez Antón. 2014. “Nonlinear Air Quality Modeling Using Multivariate Adaptive Regression Splines in Gijón Urban Area (Northern Spain) at Local Scale.” Applied Mathematics and Computation 235 (May): 50–65. https://doi.org/10.1016/j.amc.2014.02.096.

Hyndman, & Athanasopoulos, R. J. 2021. Forecasting: Principles and Practice, 3rd Edition. OTexts. http://OTexts.com/fpp3.

Nordhausen, Klaus. 2009. “The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition by Trevor Hastie, Robert Tibshirani, Jerome Friedman.” International Statistical Review 77 (3): 482–82. https://doi.org/10.1111/j.1751-5823.2009.00095_18.x.

Shen, Justin, Davesh Valagolam, and Serena McCalla. 2020. “Prophet Forecasting Model: A Machine Learning Approach to Predict the Concentration of Air Pollutants (PM_2.5, PM₁₀, O₃, NO₂, SO₂, CO) in Seoul, South Korea.” PeerJ 8 (September): e9961. https://doi.org/10.7717/peerj.9961.

Shumway, Robert H., and David S. Stoffer. 2017. Time Series Analysis and Its Applications. Springer International Publishing. https://doi.org/10.1007/978-3-319-52452-8.

---

1. El sobreajuste (overfitting en inglés) en el contexto del machine learning se refiere a un escenario en el cual un modelo se ajusta demasiado a los datos de entrenamiento y pierde su capacidad de generalización en datos nuevos e invisibles. En otras palabras, el modelo aprende y se ajusta demasiado a las particularidades y el ruido presentes en los datos de entrenamiento, en lugar de capturar los patrones y relaciones generales que se aplicarían a otros conjuntos de datos (Nordhausen 2009).